Ftyjtk

Die BDF-Verfahren (englisch Backward Differentiation Formulas) sind Mehrschrittverfahren zur numerischen Lösung von Anfangswertproblemen gewöhnlicher Differentialgleichungen:

y′(x)=f(x,y(x)),y(x0)=y0,y:R→Rn{displaystyle y'(x)=f(x,y(x)),quad y(x_{0})=y_{0},quad ycolon mathbb {R} to mathbb {R} ^{n}}

Dabei wird für y(x){displaystyle y(x)} eine Näherungslösung an den Zwischenstellen xi{displaystyle x_{i}} berechnet:

yi≈y(xi)i=1,…,m{displaystyle y_{i}approx y(x_{i})quad i=1,dotsc ,m}

Die Verfahren wurden 1952 von Charles Francis Curtiss und Joseph Oakland Hirschfelder eingeführt und sind seit dem Erscheinen der Arbeiten von C. William Gear 1971 als Löser für steife Anfangswertprobleme weit verbreitet.

Beschreibung |

Im Gegensatz zu Adams-Moulton-Verfahren wird bei BDF-Verfahren nicht die rechte Seite durch ein Interpolationspolynom approximiert, stattdessen konstruiert man ein Polynom qk{displaystyle q_{k}}, welches die letzten k{displaystyle k} Approximationen yn+1−k,…,yn{displaystyle y_{n+1-k},dotsc ,y_{n}} an die Lösung sowie den unbekannten Wert yn+1{displaystyle y_{n+1}} interpoliert:

qk(x)=∑j=0klj(x)yn+1−j{displaystyle q_{k}(x)=sum _{j=0}^{k}l_{j}(x)y_{n+1-j}}.

Hierbei sind die lj(x){displaystyle l_{j}(x)} entsprechende Lagrange-Basisfunktionen zu den äquidistant verteilten Stützstellen xn+1−k,…,xn+1{displaystyle x_{n+1-k},dotsc ,x_{n+1}}.

Man erhält ein Gleichungssystem für den unbekannten Wert yn+1{displaystyle y_{n+1}}, indem man fordert, dass das Interpolationspolynom die Differentialgleichung im Punkt xn+1{displaystyle x_{n+1}} erfüllt:

qk′(xn+1)=f(xn+1,yn+1){displaystyle q_{k}'(x_{n+1})=f(x_{n+1},y_{n+1})}.

Im Sinne der Definition allgemeiner linearer Mehrschrittverfahren definiert man nun

aj:=h⋅lj′(xn+1){displaystyle a_{j}:=hcdot l_{j}'(x_{n+1})}.

Dabei ist h=xi+1−xi{displaystyle h=x_{i+1}-x_{i}} der Abstand der Stützstellen und die konstante Schrittweite des Verfahrens. Nachdem man geeignete Startwerte y1,…,yk−1{displaystyle y_{1},dotsc ,y_{k-1}} z. B. mittels Einschrittverfahren generiert hat, erhält man die restlichen Näherungen über die lineare Rekursionsformel:

∑j=0kαjyn+1−j=h⋅f(xn+1,yn+1).{displaystyle sum _{j=0}^{k}alpha _{j}y_{n+1-j}=hcdot fleft(x_{n+1},y_{n+1}right).}

Berechnungsformeln |

Für k≤6{displaystyle kleq 6} lauten die impliziten Berechnungsformeln der BDF(k)-Verfahren:

• BDF(1) – implizites Euler-Verfahren:

yn+1−yn=hf(xn+1,yn+1){displaystyle y_{n+1}-y_{n}=hf(x_{n+1},y_{n+1})}

• BDF(2):

3yn+2−4yn+1+yn=2hf(xn+2,yn+2){displaystyle 3y_{n+2}-4y_{n+1}+y_{n}=2hf(x_{n+2},y_{n+2})}

• BDF(3):

11yn+3−18yn+2+9yn+1−2yn=6hf(xn+3,yn+3){displaystyle 11y_{n+3}-18y_{n+2}+9y_{n+1}-2y_{n}=6hf(x_{n+3},y_{n+3})}

• BDF(4):

25yn+4−48yn+3+36yn+2−16yn+1+3yn=12hf(xn+4,yn+4){displaystyle 25y_{n+4}-48y_{n+3}+36y_{n+2}-16y_{n+1}+3y_{n}=12hf(x_{n+4},y_{n+4})}

• BDF(5):

137yn+5−300yn+4+300yn+3−200yn+2+75yn+1−12yn=60hf(xn+5,yn+5){displaystyle 137y_{n+5}-300y_{n+4}+300y_{n+3}-200y_{n+2}+75y_{n+1}-12y_{n}=60hf(x_{n+5},y_{n+5})}

• BDF(6):

147yn+6−360yn+5+450yn+4−400yn+3+225yn+2−72yn+1+10yn=60hf(xn+6,yn+6){displaystyle 147y_{n+6}-360y_{n+5}+450y_{n+4}-400y_{n+3}+225y_{n+2}-72y_{n+1}+10y_{n}=60hf(x_{n+6},y_{n+6})}

Eigenschaften |

Die BDF-Verfahren sind alle implizit, da der unbekannte Wert yn+1{displaystyle y_{n+1}} in die Gleichung eingeht. BDF(k) besitzt genau die Konsistenzordnung k. Das Verfahren BDF(1) ist das implizite Euler-Verfahren. Dieses und BDF(2) sind A-stabil, die Verfahren höherer Ordnung A(α{displaystyle alpha })-stabil, wobei der Öffnungswinkel α{displaystyle alpha } sich mit höherer Ordnung verkleinert. Für k>6 sind die Verfahren instabil. Insbesondere BDF(2) ist aufgrund seiner optimalen Eigenschaften bezüglich der zweiten Dahlquist-Barriere bei der Berechnung steifer Differentialgleichungen sehr beliebt.

• Stabilitätsgebiete der BDF-Verfahren


• 
  

  

  
  

  
  

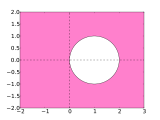
  BDF1
  

  
  

  
  


• 
  

  

  
  

  
  

  BDF2
  

  
  

  
  


• 
  

  

  
  

  
  

  BDF3
  

  
  

  
  


• 
  

  

  
  

  
  

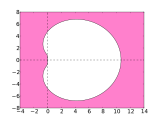
  BDF4
  

  
  

  
  


• 
  

  

  
  

  
  

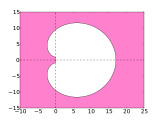
  BDF5
  

  
  

  
  


• 
  

  

  
  

  
  

  BDF6
  

  
  

  
  

Literatur |

• E. Hairer, Syvert P. Nørsett, Gerhard Wanner: Solving Ordinary Differential Equations I, Nonstiff Problems, Springer Verlag, ISBN 3540566708
  


• E. Hairer, G. Wanner: Solving Ordinary Differential Equations II, Stiff problems, Springer Verlag, ISBN 3-540-60452-9
  


• H.R. Schwarz, N. Köckler: Numerische Mathematik, Teubner (2004)


• Curtiss, Hirschfelder Integration of stiff equations, Proc. Nat. Acad. Sci. U.S.A., Band 38, 1952, 235–243.

Weblinks |

• Gear, Backward Differentiation Formulas, Scholarpedia